A - 106
枚举 \(3\) 的次幂,看一下差是否是 \(5\) 的次幂。
B - Values
可以发现一个连通块内值可以任意变化,所以只需要 check 每个连通块的 \(\sum a\) 和 \(\sum b\) 是否相等。
C - Solutions
可以发现,按 \(r\) 排序是正解,同时按 \(l\) 排序答案至少也是 \(1\),如果答案 \(=m\),则两个算法都能得到正确答案,所以把 \(m<0\) 和 \(m\geqslant n-1\) 特判掉,注意这里还需要特判 \(n=1\)。
其他情况构造如下:
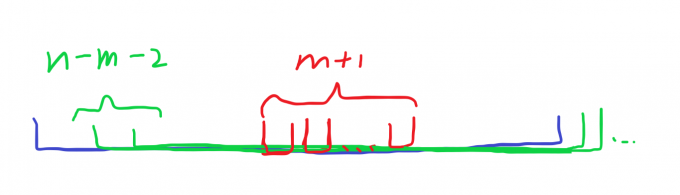
D - Powers
\[ \begin{aligned} &\sum\limits_{l=1}^{n-1}\sum\limits_{r=l+1}^n(a_l+a_r)^k\\ =&\sum\limits_{l=1}^{n-1}\sum\limits_{r=l+1}^n\sum\limits_{i=0}^k\binom{k}{i}a_l^ia_r^{k-i}\\ =&\left(k!\sum\limits_{i+j=k}\frac{\sum a^i}{i!}\frac{\sum a^j}{j!}-\sum\limits_{i=1}^n(2i)^k\right)\div2 \end{aligned} \]
这个是个卷积的形式,可以 \(O(nk)\) 求出幂次和的 EGF 然后 \(O(k^2)\) 卷积求解。
E - Medals
把人和上班的点做二分图匹配,考虑二分答案,答案有一个上界 \(2nk\),因为这时每一个点都向至少 \(nk\) 个点连边,根据 hall 定理此时一定有解。
现在考虑如何判一般情况是否有解,仍旧使用 hall 定理,我们判断任何一个雇员的子集可匹配的天数是否都大于等于雇员数乘 \(k\),我们容斥一下计算没有被这个集合中的任何一个雇员连边的天数。为此,我们对每条边先计算出没有向这条边连的人的集合 \(g_i\),假设当前二分的天数是 \(x\),对所有 \(i=0\rightarrow x-1\)(认为从第 \(0\) 天开始),令 \(f_{g_i}\) 加 \(1\),然后注意到每个集合要加上所有包含这个集合的答案,这个使用高维后缀和解决(FWTand)。所以总复杂度为 \(O(k2^n+n2^n\log(nk))\)。
F - Figures
考虑 prufer 序列,给其编一个组合意义:每个部分先任意选一个接口,然后再任意选 \(n-2\) 个接口,所以答案为 \[ \left(\prod d_i\right)\left(\sum (d_i-1)\right)^{\underline{n-2}} \] 也可以数学推导,不难发现我们需要求的是这个 \[ (n-2)![x^{n-2}]\prod\limits_{i=1}^n\sum\limits_{j=0}^{d_i}\frac{d_i!}{j!(d_i-j-1)!}x^j \] 即枚举每个数在 prufer 序列的出现次数,注意同一个 part 的连接点选择是有顺序的,所以后面不是 \(\dfrac{d_i!}{(j+1)!(d_i-j-1)!j!}\)。
然后是推式子时间 \[ \begin{aligned} &(n-2)![x^{n-2}]\prod\limits_{i=1}^n\sum\limits_{j=0}^{d_i}\frac{d_i!}{j!(d_i-j-1)!}x^j\\ =&(n-2)![x^{n-2}]\prod_{i=1}^nd_i\sum\limits_{j=0}^{d_i}\frac{(d_i-1)!}{j!(d_i-j-1)!}x^j\\ =&(n-2)![x^{n-2}]\prod_{i=1}^nd_i\sum\limits_{j=0}^{d_i}\binom{d_i-1}{j}x^j\\ =&(n-2)![x^{n-2}]\prod_{i=1}^nd_i(1+x)^{d_i-1}\\ =&(n-2)!\prod_{i=1}^nd_i[x^{n-2}](1+x)^{\sum (d_i-1)}\\ =&(n-2)!\prod_{i=1}^nd_i\binom{\sum d_i -n}{n-2}\\ =&\prod_{i=1}^n d_i\left(\sum\limits_{i=1}^n d_i-n\right)^{\underline{n-2}} \end{aligned} \]