给定 \(n\) 个点 \(m\) 条边的无向图,每条边有两个权值 \(a_i,b_i\),求一棵生成树使得 \[ \left(\sum\limits_{e\in T} a_e\right)\left(\sum\limits_{e\in T} b_e\right) \] 最小,输出乘积最小时的 \(\sum\limits_{e\in T} a_e\) 和 \(\sum\limits_{e\in T} b_e\)。\(n\leqslant 200\),\(m\leqslant 10000\),\(0\leqslant a_i,b_i\leqslant 255\),\(a_i,b_i\in N\)。
对于任意一棵生成树,我们把其映射到平面直角坐标系中的一个点 \((\sum a_e,\sum b_e)\),那么我们所求即为 \(xy\) 最小的点。我们不难发现它一定在所有点构成的左下凸壳上。
我们先分别令 \(a_e=0\) 和 \(b_e=0\),这样求出的是只有一种权值时的最小生成树,故其横/纵坐标一定最小,所以这两个点一定在凸包上(更精确的说,左下凸壳的两个端点)。
然后,我们考虑所有还可能在凸壳上的点,设刚才确定的两个点为 \(A,B\),则如果一个点 \(C\) 可能成为凸壳上的点,其一定在 \(AB\) 的左下方。同时,在 \(AB\) 左下方距离 \(AB\) 最远的点一定在凸壳上,所以我们考虑求出这个距离 \(AB\) 最远的点 \(C\)。
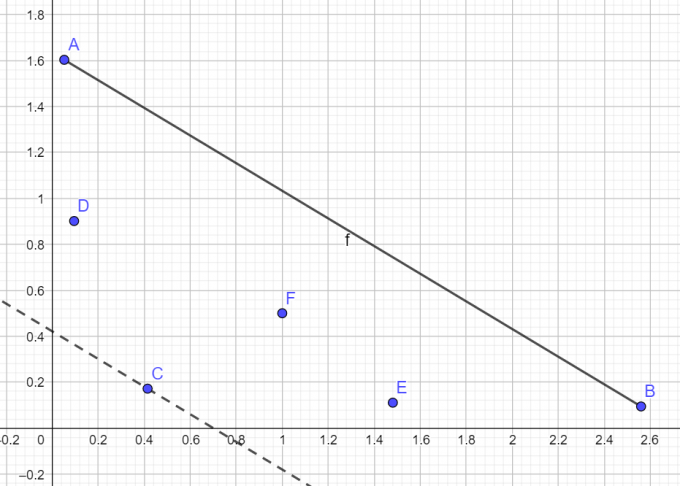
如图所示(其实每个点都应该是整点,我没画好),我们现在已知 \(A,B\) 的坐标,想要求出这个点 \(C\),换句话说,我们要找到那个使得 \(\triangle ABC\) 的面积最大的点。假设 \(A,B,C\) 的坐标分别为 \((x_A,y_A),(x_B,y_B),(x_C,y_C)\),则 \(S_{\triangle ABC}=-\dfrac{1}{2}(\overrightarrow{AB}\times \overrightarrow{AC})\) ,故我们需要让 \(\overrightarrow{AB}\times \overrightarrow{AC}\) 最小。下面我们来推一下式子: \[ \begin{aligned} &\overrightarrow{AB}\times \overrightarrow{AC}\\ =&(x_B-x_A)(y_C-y_A)-(x_C-x_A)(y_B-y_A)\\ =&x_By_C-x_By_A-x_Ay_C+x_Ay_A-x_Cy_B+x_Cy_A+x_Ay_B-x_Ay_A\\ =&(x_B-x_A)y_C+(y_A-y_B)x_C-x_By_A+x_Ay_B \end{aligned} \] 后两项是常数,所以我们要让 \((x_B-x_A)y_C+(y_A-y_B)x_C\) 最小,只需要对每条边 \(e\),将 \(v_e\) 设为 \((y_A-y_B)a_e+(x_B-x_A)b_e\),然后求最小生成树得到的那棵树即为点 \(C\)。这里可能有多个点 \(C\) 在同一条直线的情况,但是并不重要。
然后,我们看刚才那张图,\(D,E\) 也是凸壳上的点,所以我们要对 \(AC,BC\) 递归做下去,直到当前直线左下方没有点,也就是叉积大于等于 \(0\),最后取所有点的最小值。
考虑分析复杂度,刚才那个过程实际上是一个叫做 quick hall 的求凸包算法。不难发现,我们一共做了 \(O(凸壳上的点数)\) 次最小生成树。由于所有生成树对应的点都是整点,而且点数远远高于值域范围 \(na\),据 EI 说此时凸壳上的点数最大是 \(O((na)^{\frac{2}{3}})\) 的,所以总复杂度为 \(O(n^{\frac{8}{3}}a^{\frac{2}{3}})\)(prim 实现 MST)。
顺便说两句废话,如果边权不一定为整数但是非负,也可以证明做 MST 的次数是 \(O(m^2)\) 的;如果边权可能为负,那么这个应该没有多项式做法。
代码(比较懒所以写了 kruskal 多一个 \(\log\)):
1 |
|