美食家
我们很容易写出朴素的 dp 方程,设 \(f(i,u)\) 为第 \(i\) 天在城市 \(u\) 能得到的最大愉悦值之和,那么有转移: \[ f(i,u)=\max_{(v,u)\in E}f(i-w_{(v,u)},v)+c_u \]
如果某一个某一次美食节被举办,那么就往对应的 \(f\) 加上 \(y_i\)
我们注意到 \(w\) 很小,并且 \(\max\) 对 \(+\) 有分配律,所以我们可以矩阵快速幂加速计算,我们考虑向量: \[ \begin{bmatrix} f(t,1)\\ f(t,2)\\ \vdots\\ f(t,n)\\ f(t-1,1)\\ \vdots\\ f(t-4,n) \end{bmatrix} \] 这个东西可以通过 \[ \begin{bmatrix} f(t-1,1)\\ f(t-1,2)\\ \vdots\\ f(t-1,n)\\ f(t-2,1)\\ \vdots\\ f(t-5,n) \end{bmatrix} \] 左乘转移矩阵得到。转移矩阵比较显然,大概是每有一条边 \((u,v,w)\) 就把 \((v,u+(w-1)n)\) 改为 \(c_v\),然后其余地方是 \(-inf\)。这样总复杂度是 \(O(n^3w^3k\log T)\) 无法通过,只需要预处理转移矩阵的次幂,然后每一次只需要向量乘矩阵,总复杂度为 \(O((n^3w^3+kn^2w^2)\log T)\),可以通过。
代码:
1 |
|
命运
我们在一条链的底部加入这条链的限制。考虑 dp,设 \(f(u,t)\) 为以 \(u\) 为根的子树,目前尚未满足并且已经被加入的链中,最深的链顶的深度为 \(t\) 的方案数。特殊的,当所有限制都被满足,方案数被记在 \(f(u,0)\) 中。则答案为 \(f(1,0)\)。
那么我们考虑加入一个子树 \(v\) 的答案,不难发现有转移 \[ \begin{aligned} f'(u,t)&=\sum\limits_{\max(x,y)=t}f(u,x)f(v,y)+f(u,t)\sum\limits_{y\leqslant deep_u}f(v,y)\\ &=f(u,t)\left(\sum\limits_{y=0}^tf(v,y)+\sum\limits_{z=0}^{deep_u}f(v,z)\right)+f(v,t)\sum\limits_{x=0}^{t-1}f(u,x)\\ &=f(u,t)(s(v,t)+s(v,deep_u))+f(v,t)s(u,t-1)\\ \end{aligned} \] 其中 \(s\) 是前缀和。这个转移叫做 “max 卷积”,这个东西看上去难以维护,怎么优化我们一会再说。
合并完所有子树之后我们对每一个点需要增加以这个点为底的限制,设 \(maxd_u\) 为以 \(u\) 为起点的所有链中链顶最深的节点的深度,那么则 \[ f'(u,t)= \begin{cases} f(u,t)&t> maxd_u\\ \sum\limits_{x=0}^{maxd_u}f(u,x) &t=maxd_u\\ 0 &t<maxd_u \end{cases} \] 接下来我们说怎么优化这个 dp。先做 max 卷积。max 卷积可以通过线段树合并来实现:具体地,我们合并的时候,维护两个标记 \(s1,s2\) 分别表示 \(s(v,l-1)+s(v,deep_u)\) 和 \(s(u,l-1)\),那么当递归到叶子节点时,直接按照标记这个乘一下;当某一个区间只在一棵树中存在时,是一个区间乘的形式;剩下的情况先把左儿子的 \(sum\) 加到标记上,递归右儿子,再用之前的标记递归左儿子,最后合并答案即可。
然后合并完所有的子树,加入新的限制时,相当于区间查询、区间修改和新增一个节点,都可以使用线段树维护。复杂度的话,由于每一个限制至多新增一个节点,所以一开始所有线段树的总结点数是 \(O(n\log n)\) 的(这里认为 \(n,m\) 同阶),然后合并时如果某一个节点在合并中的两棵树都存在,总结点数会 \(-1\),而只在一棵树中存在的情况和都存在的情况次数是同阶的,所以总复杂度为 \(O(n\log n)\)。
代码:
1 |
|
时代的眼泪
这个是标程做法,但是实现起来比直接分块要麻烦所以没有写代码(其实就是复述了一遍 ppt /kk,如果有误麻烦指出)。
如非特殊说明,复杂度分析认为 \(n,m\) 同阶。
我们考虑对平面建立树套树(线段树套动态开点线段树)。那么内层的每个节点代表了平面中的一个矩形,为了之后的计算,我们需要维护树套树中每个矩形内部的答案。
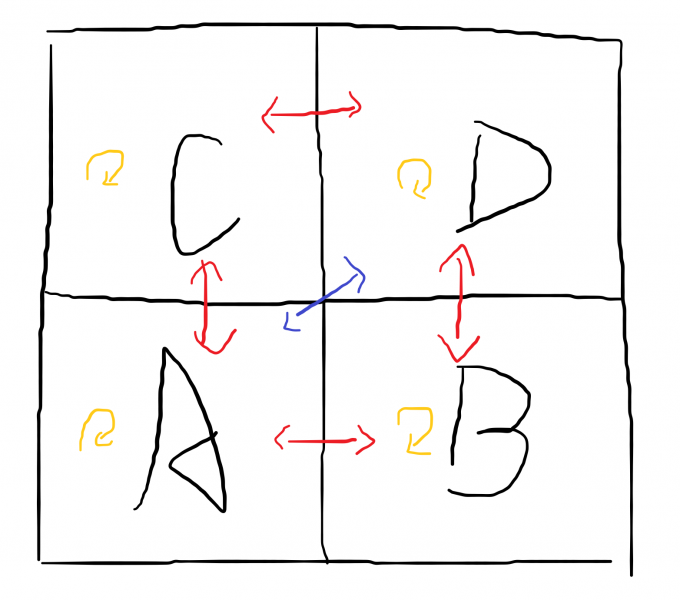
如图,假设我们现在有一个长和宽均不为 \(1\) 的矩形(当至少一维为 \(1\) 时答案一定为 \(0\)),我们想要求出这个矩形的答案(我们认为左下角为较小的下标),我们把这个矩形一分为四,并且我们已经递归得出了每个子矩形的答案,那么我们有: \[ \begin{aligned} ans(ABCD)=&ans(AB)+ans(CD)+ans(AC)+ans(BD)\\ -&ans(A)-ans(B)-ans(C)-ans(D)+siz(A)\cdot siz(D) \end{aligned} \] 其中 \(siz(A)\) 是 \(A\) 中包含点的数量。这个东西本质就是枚举任意两块,求出块之间的答案,再求出块内部的答案。由于 \(ans(AB)\) 已经包含了 \(ans(A)+ans(B)\),所以这里要容斥捡回去。本题可以这样分治的关键在于 \(A\) 和 \(D\) 的贡献是平凡的。
子矩形的 \(ans\) 我们可以通过子树查询得到,\(siz\) 我们只需要顺便维护就好了。
现在我们考虑回答询问。首先,我们需要用 \(O(\log^2n)\) 个在树套树中的矩形定位出询问矩形,如下图所示:
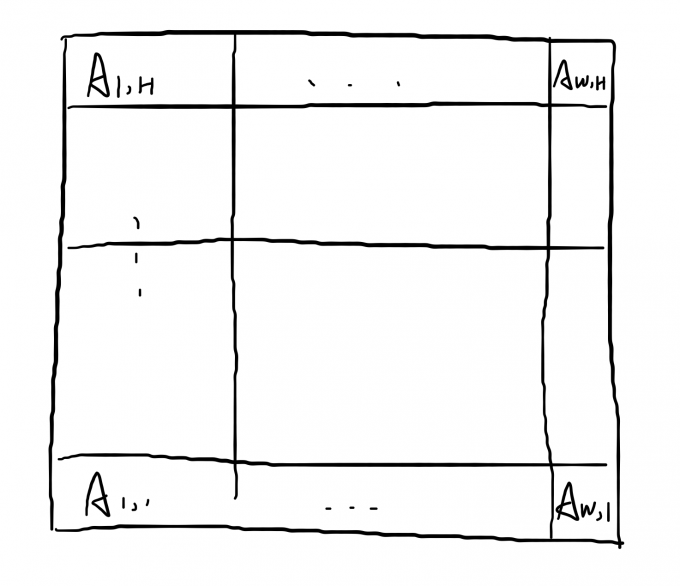
其中每一个 \(A_{i,j}\) 都是树套树中的矩形。那么我们用类似上面的容斥来计算答案:即求出每行和每列的答案,加上行列均不同的两块的贡献,再减去每一块内部的答案。那么有 \[ \begin{aligned} ans(1\dots w,1\dots h)=&\sum\limits_{i=1}^w\sum\limits_{j=1}^hsiz(i,j)\sum\limits_{c=i+1}^w\sum\limits_{d=j+1}^hsiz(c,d)\\ +&\sum\limits_{i=1}^wans(i,1\dots h)+\sum\limits_{i=1}^hans(1\dots w,i)\\ -&\sum\limits_{i=1}^w\sum\limits_{j=1}^hans(i,j) \end{aligned} \] 第一行和第三行我们直接在树套树上查询就可以了,注意第二行,我们发现这实际上仍旧是一个值域范围内的区间顺序对,但是这里值域范围一定出现在了树套树上,即只有 \(O(n\log n)\) 种。并且如果这是一个 \(w\times n\) 的矩形,由于我们给定的是一个排列,所以这个矩形内的数只有 \(w\) 个。这样我们在这样的矩形查一次的复杂度是 \(O(\sqrt w)\) 的,由于每一个长度的矩形只会出现 \(O(1)\) 次,所以一次查询的总复杂度是 \(O(\sqrt n+\sqrt{\frac{n}{2}}+\sqrt{\frac{n}{4}}+\dots)=O((1+\frac{1}{\sqrt 2}+\frac{1}{2}+\dots)\sqrt n)=O(\sqrt n)\) 的。预处理的复杂度类似,所以这个算法的总复杂度是 \(O(n\log^2n+T)\)(\(T\) 指区间逆序对复杂度)的,空间上如果用一般的树套树也是 \(O(n\log^2n+T)\) 的。据官方题解说也可以做到一个 \(\log\) 或者线性。
据 lxl 说,这样分治套分块似乎当分块的复杂度比 \(O(n^{1.5})\) 低时才会更优秀。
制作菜品
通过观察样例和数据范围,我们可能有一个猜想:当 \(m\geqslant n-1\) 时一定有解,这个结论我们可以通过归纳法证明:当 \(n\leqslant 2\) 时显然成立,当 \(n>2\) 时,我们取剩余质量最小的食材,如果质量 \(\geqslant k\),那么一定有 \(m\geqslant n\),那么我们把这道菜全部用这个食材做,那么 \(m\) 减小 \(1\),依旧满足 \(m\geqslant n-1\);如果质量 \(<k\),我们再取质量最大的菜,不难证明两种菜的质量加起来一定 \(\geqslant k\),这样就相当于把第一种菜用掉,然后剩余要做的菜 \(-1\),即 \(m,n\) 均减小 \(1\),依旧满足 \(m\geqslant n-1\)。
然后我们考虑 \(m=n-2\) 的情况,也不难有猜想:只有能够划分为两个 \(m=n-1\) 的集合的时候有解。充分性显然,考虑必要性:当 \(m=1,n=3\) 时无解,如果不能划分为两个 \(m=n-1\) 的集合,那么每做一盘菜质量减为 \(0\) 的食材数量一定 \(\leqslant1\)(要不然我们就找到了一组划分),这样一直保持 \(m\leqslant n-2\),所以一定无解。
那么对于 \(m\geqslant n-1\) 的情况,我们随便写个模拟就好了,对于 \(m=n-2\) 的情况,如果我们设每种食材的权值为 \(d_i-k\),那么就相当于问有没有一个子集的权值和为 \(-k\),这是一个可行性背包,可以使用 bitset 优化,复杂度为 \(O(\frac{n^2k}{w})\),输出方案只需要找到的时候往前递归找就可以了。
代码(由于未知原因,这份代码在 windows 下似乎会 RE):
1 |
|
超现实树
设森林中最深的树的深度为 \(h\)。我们定义一棵树为好的当且仅当对于每个节点,左右儿子的 \(size\) 的较小值小于等于 \(1\) (如果为空那么 \(size=0\)),不难发现好树的形态一定是一条主链,然后链上每个点可能额外接了一个单独的节点。那么有以下结论:这个森林是几乎完备的当且仅当所有深度 \(\leqslant h\) 的好的树都可以被生成。因为每一棵树都可以由至少一棵好树生成(把单独的叶子变成一棵树),如果有一棵好树无法被生成,一定存在一个叶子使得无论把叶子替换成什么树都无法生成(感性理解一下吧)。
这样,在给定的森林中,如果不是好的树,那么它一定没用(因为它无法生成任何一棵好树)。
我们递归判断一个森林是否是几乎完备的,如果为空,那么返回否,如果有单个节点的是,返回是,否则遍历每一棵树,可能分为以下情况:
- 根节点只有左子树,这时把根节点的左子树加入这种情况的集合中
- 根节点只有右子树,这时把根节点的右子树加入这种情况的集合中
- 根节点有左子树,且右子树大小为 \(1\),这时把根节点的左子树加入这种情况的集合中
- 根节点有右子树,且左子树大小为 \(1\),这时把根节点的右子树加入这种情况的集合中
- 根节点的左右子树大小均大于 \(1\),这时忽略这棵树
显然每一棵树最多符合两种条件(当左右子树大小都为 \(1\) 时同时满足 2,3),那么这个森林完备当且仅当前四种递归计算下去均满足,因为如果有一种不满足,我们等价于找到了一棵深度 \(\leqslant h\) 的好树。这样一开始预处理好每个点的 \(size\),每个点只会造成 \(O(1)\) 贡献,总复杂度为 \(O(\sum n)\)。
代码:
1 |
|