0%

「NOI2019」序列

发表于 阅读次数： Valine：

给定两个长为 \(n\) 的正整数序列 \(\{a_n\},\{b_n\}\)，现在让你在每个序列中都选 \(k\) 个下标，并且在两个序列中都被选中的下标个数不少于 \(L\)，最大化选中的下标对应的数之和。\(n\leqslant 2\times 10^5\)。

我们认为一次操作为各选中 \(a\) 和 \(b\) 中的一个未被选中的下标。我们发现两个序列中都被选中的下标个数不少于 \(L\)，等价于最多 \(k-L\) 次操作选中的下标不同。这样我们可以建出一个费用流模型：

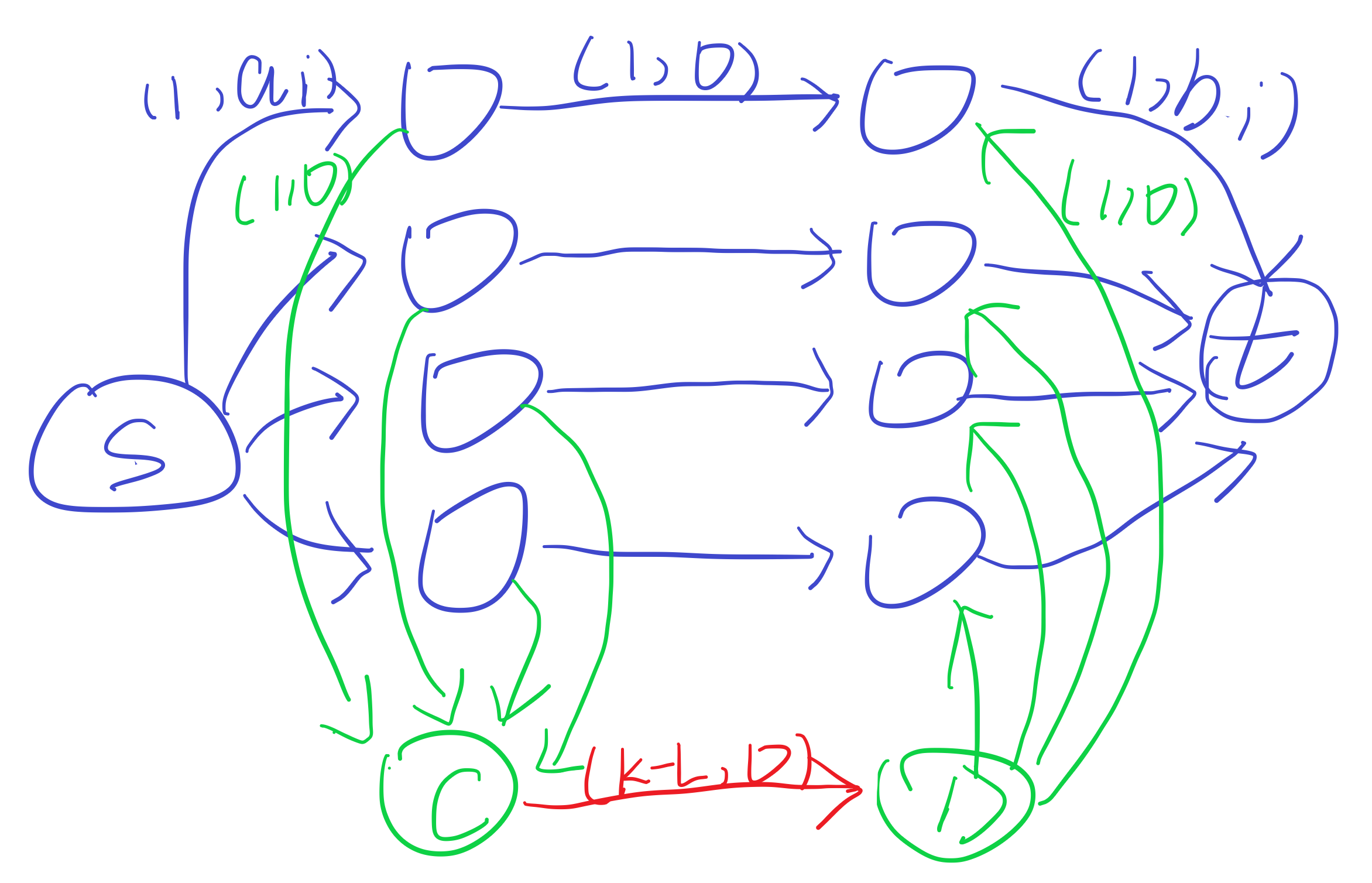
括号里的是边权，第一个数是流量大小，第二个数是费用，同类边只标注了一次边权，这样 \(s\) 到 \(t\) 的流量恰好为 \(k\) 时的费用就是答案。这个算法的正确性比较显然，只有通过红色边才能增广出 \(a\) 与 \(b\) 下标不同的情况，而最多只能进行 \(k-L\) 次这样的增广，而且我们每一次单路增广增加的流量一定为 1。

如果直接写一个 SPFA 费用流，这样的复杂度为 \(O(nmk)\)，实际跑不满似乎可以拿到 64 分。

然后是重头戏模拟费用流部分。首先我们定义红边的剩余流量为自由流的大小。很显然，如果自由流有剩余，那么一次增广通过红边增广的权值一定最大，因为它可以覆盖任何匹配。

我们考虑增广的情况：

  1. 通过 \(C,D\) 增广了一条 \(a\) 和 \(b\) 的下标不同的情况。（如果增广了下标相同的点我们可以归为第二种情况，也就是不要白消耗自由流了），这等价于匹配了一对下标不同的数。

  2. 直接走一条 \(s\rightarrow a_i\rightarrow b_i\rightarrow t\) 的增广路，这等价于匹配了一对下标相同的数。

  3. 考虑退流，走了一条 \(s\rightarrow a_i\rightarrow C\rightarrow a_j\rightarrow b_j\rightarrow t\) 的增广路，设原来和 \(a_j\) 匹配的为 \(b_k\)，那么这等价于把原来的 \(a_j-b_k\) 这个匹配取消，然后新添加 \(a_j-b_j\) 和 \(a_i-b_k\) 两对匹配。这样会使匹配数量增加 1，自由流数量不变或 \(+1\)（具体情况见后面）。

  4. 类似情况 3，走一条 \(s\rightarrow a_j\rightarrow b_j\rightarrow D\rightarrow b_i\rightarrow t\) 的增广路，这等价于把 \(a_k-b_j\) 这个匹配取消，新增 \(a_j-b_j\) 和 \(a_k-b_i\) 两对匹配。

这样，我们开一个变量 left 记录自由流的大小，如果还有自由流，我们优先用自由流，因为一定不劣。否则，我们选择剩下几种方案中权值最高的那个。

实现上，我们需要开 5 个堆，分别维护未匹配的 \(a_i/b_i\) 的值，未匹配的 \(a_i+b_i\) 的值，匹配过但是没有固定（指这个点不通过红色边增广，显然，如果一个点通过了蓝色边增广，那么它的匹配一定不会变）的 \(a_i/b_i\) 所对应的 \(b_i/a_i\) 的值。然后有一些操作会导致自由流变多，下面列出来：

下面认为橙色为现在匹配的两个点：

情况1
情况2

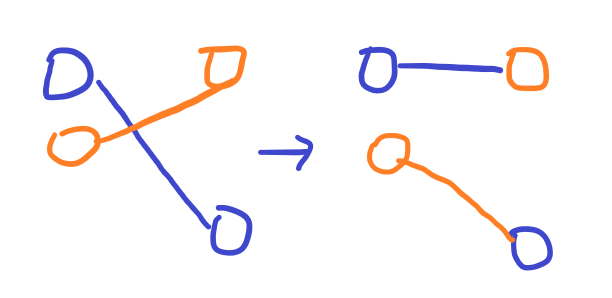
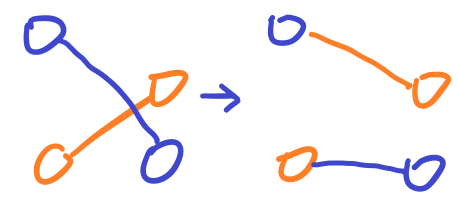
如果是类型 1，那么自由流额外 +1（我们认为只要出现一次类型 1，自由流都减小 1，也就是说这样等价于自由流大小最终没有变化），要不然就是类型 3 或 4，这种情况自由流不变。

情况3
情况4

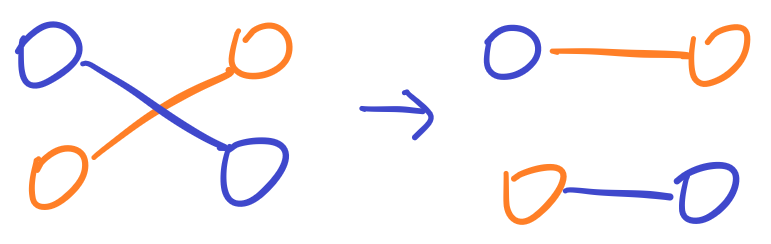
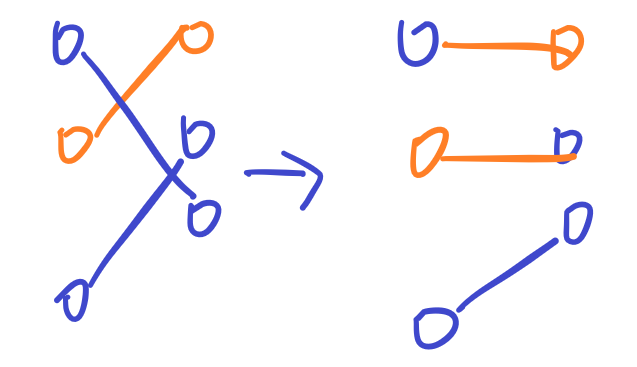
这两种情况（本质上是一种，即现在匹配的两个点在另外一个序列中都被匹配过了）出现在类型 1 时，自由流额外 +2；出现在类型 3 或 4 时，自由流额外 +1。

至于如何判断，我们开两个数组记录每个数是否被增广过，同时这个作为懒惰删除的标记，如果不明白代码不是很长可以看代码。

由于我们每一次的操作都等价于在费用流图中的增广，且每次都是最长路，所以这个算法是正确的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include<bits/stdc++.h>
#define mp make_pair
using namespace std;
namespace input
{
    const int InputBufferSize=(1<<25)+5;
    char buffer[InputBufferSize],*s,*eof;
    inline void init()
    {
        assert(stdin!=NULL);
        s=buffer;
        eof=s+fread(buffer,1,InputBufferSize,stdin);
    }
    inline bool read(int &x)
    {
        x=0;
        int flag=1;
        while(!isdigit(*s)&&*s!='-')s++;
        if(eof<=s)return false;
        if(*s=='-')flag=-1,s++;
        while(isdigit(*s))x=x*10+*s++-'0';
        x*=flag;
        return true;
    }
}
using namespace input;
typedef long long ll;
typedef pair<int,int> pii;
priority_queue<pii>q1,q2,q3,q4,q5;
int a[200005],b[200005];
bool visited[200005],visited2[200005];
int main()
{
    init();
    int _;
    read(_);
    while(_--)
    {
        a[0]=b[0]=-1e9;
        while(!q1.empty())q1.pop();
        while(!q2.empty())q2.pop();
        while(!q3.empty())q3.pop();
        while(!q4.empty())q4.pop();
        while(!q5.empty())q5.pop();
        int n,k,l,left;
        ll ans=0;
        read(n),read(k),read(l);
        left=k-l;
        for(int i=1;i<=n;i++)read(a[i]),q1.push(mp(a[i],i)),visited[i]=visited2[i]=0;
        for(int i=1;i<=n;i++)read(b[i]),q2.push(mp(b[i],i)),q3.push(mp(a[i]+b[i],i));
        while(k--)
        {
            if(left)//类型 1
            {
                while(visited[q1.top().second])q1.pop();
                while(visited2[q2.top().second])q2.pop();
                int x=q1.top().second,y=q2.top().second;
                q1.pop(),q2.pop();
                ans+=a[x]+b[y];
                if(x!=y)
                {
                    left--,left+=visited2[x]+visited[y];
                    if(!visited2[x])q5.push(mp(b[x],x));
                    else q4.pop();
                    if(!visited[y])q4.push(mp(a[y],y));
                    else q5.pop();
                }
                visited[x]=visited2[y]=1;
            }
            else
            {
                while(visited[q1.top().second])q1.pop();
                while(visited2[q2.top().second])q2.pop();
                while(visited[q3.top().second]||visited2[q3.top().second])q3.pop();
                int r=q3.top().second,s1=q4.empty()?0:q4.top().second,s2=q2.top().second,t1=q5.empty()?0:q5.top().second,t2=q1.top().second;
                if(a[r]+b[r]>=a[s1]+b[s2]&&a[r]+b[r]>=b[t1]+a[t2])//类型2
                {
                    visited[r]=visited2[r]=1;
                    ans+=a[r]+b[r];
                }
                else if(a[s1]+b[s2]>=b[t1]+a[t2])//类型3
                {
                    ans+=a[s1]+b[s2];
                    visited[s1]=visited2[s2]=1;
                    q2.pop(),q4.pop();
                    if(visited[s2])left++,q5.pop();
                    else q4.push(mp(a[s2],s2));
                }
                else//类型4
                {
                    ans+=b[t1]+a[t2];
                    visited2[t1]=visited[t2]=1;
                    q1.pop(),q5.pop();
                    if(visited2[t2])left++,q4.pop();
                    else q5.push(mp(b[t2],t2));
                }
            }
        }
        printf("%lld\n",ans);
    }
    return 0;
}