0%

「USACO19FEB」Mowing Mischief P

发表于 更新于 阅读次数： Valine：

给你一个长、宽均为 \(T\) 的网格图，左下角坐标为 \((0,0)\)，右上角坐标为 \((T,T)\)。现在图上面有 \(n\) 个点（一定在格点上），你需要选择一些点，使得你选择的点按 \(x\) 从小到大排序后 \(y\) 也单调上升。最大化选的点的数量；在此基础上，让排序好的相邻的两点形成的矩形的面积之和最小。输出最小面积和。\(T\leqslant 10^6,N\leqslant 2\times 10^5\)。

首先，对于最大化选点的数量，这可以看作按 \(x\) 排好序之后求一遍 LIS。为了方便，我们把按 \(x\) 排完序的点重编号，以后认为 \(i<j\) 等价于 \(x_i<x_j\)（题目保证了不存在两个点使得 \(x\) 或 \(y\) 相等）。我们设 \(l_i\) 为以 \(i\) 结尾的 LIS 的长度。

第二问比较明显还需要 dp 求解，为了保证选的点数最多，我们只能在 \(l\) 值相差为 \(1\) 的点之间进行转移。具体地，设 \(f[i]\) 为选择了以 \(i\) 为结尾的 \(l_i\) 个点矩形面积和的最小值，那么转移显然： \[ f[i]=\min_{l_i=l_j+1,j<i,y_j<y_i}f[j]+(x_i-x_j)(y_i-y_j) \] 这样就有了一个 \(O(n^2)\) 的朴素算法。

这个东西可能看起来有一些像斜率优化，但是并不行，因为拆开括号以后既有 \(x_iy_j\) 项又有 \(x_jy_i\) 项，斜率优化做不了这个。

我们考虑另外一个优化办法——决策单调性。我们先把括号拆开： \[ f[i]=\min_{l_i=l_j+1,j<i,y_j<y_i}f[j]+x_iy_i-x_iy_j-x_jy_i+x_jy_j \] 假设现在有两个决策点 \(j,k\ (j<k)\)，正在进行决策的是 \(i\)，那么 \(j\) 比 \(k\) 优当且仅当 \[ f[j]+x_iy_i-x_iy_j-x_jy_i+x_jy_j\leq f[k]+x_iy_i-x_iy_k-x_ky_i+x_ky_k\\ f[j]-x_iy_j-x_jy_i+x_jy_j\leq f[k]-x_iy_k-x_ky_i+x_ky_k\\ (y_k-y_j)x_i+(x_k-x_j)y_i\leq f[k]-f[j]+x_ky_k-x_jy_j \] 我们注意到，对于两个 \(l\) 相同的点 \(j,k\)，若 \(x_j<x_k\)，那么一定有 \(y_j>y_k\)。因为如果依旧有 \(y_j<y_k\) 那么 \(l_k\) 就可以从 \(l_j\) 转移过来，它们的 \(l\) 就不相等了。反过来同理。

那么如果我们把 \(x_i\)，\(y_i\) 看作变量，那么 \(j\) 比 \(k\) 优的情况对应了坐标系里的一个半平面（也就是不等式的解集），而且因为我们钦定 \(j>k\)，那么这个半平面一定长这个样子

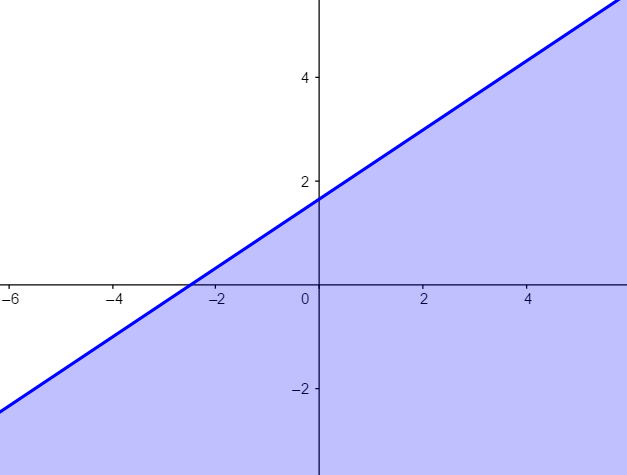
其中蓝色为解集部分，解集一定是一条斜率为正的直线的下方。那么要更新的点一定被这条直线分为了两部分。那么如果在 \(i\) 时，\(j\) 比 \(k\) 优（即点 \(i\) 在蓝色区域内），那么对于 \(u>i\)，\(j\) 也一定比 \(k\) 优。这样的话对于一组 \(l\) 相同的询问，他们的最优决策位置一定是单调不增的。这就可以决策单调性了。

注意一下上面的分析都忽略了 \(x\) 和 \(y\) 的限制，那么如何满足呢？注意到对于任何一个点，可行的决策点都是一个区间，所以对每一排开一个线段树，线段树分治一下，把询问丢到所有符合要求的区间内，这样如果一个询问被挂在了某个区间内，区间内的点都可以转移到它，最后把答案取 \(\max\) 就好了。如果以分治或者二分+单调队列计算决策单调性，总的复杂度为 \(O\left(n(\log^2n+\log T)\right)\)。

需要特殊注意的是每次计算一个区间时，不要直接和 \(f[mid]\) 比较，需要再开一个变量记录只包含这段区间中的决策点时的最小值，要不然有时已经算过的 \(f[mid]\) 比整个区间的决策都优，这样就会错误。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
struct flower
{
    int x,y,ans;
}c[200015];
typedef long long ll;
ll const inf=1e12;
int tree[1000005],T;
ll f[200015];
void modify(int x,int y){x++;for(int i=x;i<=T+1;i+=(i&(-i)))tree[i]=max(tree[i],y);}
int ask(int x){x++;int res=0;for(int i=x;i;i-=(i&(-i)))res=max(res,tree[i]);return res;}
bool cmp(flower x,flower y){return x.x<y.x;}
vector<int>v[200015],buc[1000005];
void insert(int l,int r,int x,int id,int d)
{
    if(c[v[d-1][l]].x>c[id].x||c[v[d-1][r]].y>c[id].y)return;
    if(c[v[d-1][l]].x<c[id].x&&c[v[d-1][l]].y<c[id].y&&
       c[v[d-1][r]].x<c[id].x&&c[v[d-1][r]].y<c[id].y){buc[x].pb(id);return;}
    int mid=(l+r)>>1;
    insert(l,mid,x*2,id,d);insert(mid+1,r,x*2+1,id,d);
}
void solve(int ql,int qr,int l,int r,int x,int d)
{
    if(l>r)return;
    int mid=(l+r)>>1,id=0;
    ll val=inf;//注意这里
    for(int i=ql;i<=qr;i++)
        if(f[v[d-1][i]]+1ll*(c[buc[x][mid]].x-c[v[d-1][i]].x)*
        (c[buc[x][mid]].y-c[v[d-1][i]].y)<val)
            val=f[v[d-1][i]]+1ll*(c[buc[x][mid]].x-c[v[d-1][i]].x)*
        (c[buc[x][mid]].y-c[v[d-1][i]].y),id=i;
    f[buc[x][mid]]=min(f[buc[x][mid]],val);
    solve(id,qr,l,mid-1,x,d);solve(ql,id,mid+1,r,x,d);//注意x是不变的
}
void dfs(int l,int r,int x,int d)
{
    solve(l,r,0,buc[x].size()-1,x,d);
    buc[x].clear();
    if(l==r)return;
    int mid=(l+r)>>1;
    dfs(l,mid,x*2,d),dfs(mid+1,r,x*2+1,d);
}
inline int read()
{
    int x=0;
    char ch=getchar();
    while(!isdigit(ch))ch=getchar();
    while(isdigit(ch))x=x*10+ch-48,ch=getchar();
    return x;
}
int main()
{
    int n;
    n=read(),T=read();
    for(int i=1;i<=n;i++)c[i].x=read(),c[i].y=read();
    n+=2;
    c[n].x=c[n].y=T;
    sort(c+1,c+n+1,cmp);
    int t=0;
    for(int i=1;i<=n;i++)
        c[i].ans=ask(c[i].y)+1,modify(c[i].y,c[i].ans),v[c[i].ans].pb(i);
    for(int i=1;i<=n;i++)t=max(t,c[i].ans),f[i]=(c[i].ans==1?0:inf);
    for(int i=2;i<=t;i++)//处理第i层
    {
        for(auto j:v[i])insert(0,v[i-1].size()-1,1,j,i);//线段树分治
        dfs(0,v[i-1].size()-1,1,i);//计算答案
    }
    ll ans=inf;
    for(int i=1;i<=n;i++)if(c[i].ans==t)ans=min(ans,f[i]);
    printf("%lld",ans);
    return 0;
}