求基环树随机点分治总遍历次数期望
基环树随机点分治步骤:
①遍历当前分治区域所有点一次
②在当前分治区域随机选择一个点 \(x\)
③将 \(x\) 删掉,产生的所有连通块递归处理。
\(n\leqslant 3000\)
按照套路,我们先考虑如果是一棵树的情况,再扩展到基环树的情况。不难发现如果我们把分治过程建成点分树,那么我们实际上求的是 \(\sum\limits_xsize_x\) 的期望,其中 \(size_x\) 是 \(x\) 子树的大小。 根据期望的线性性,我们考虑计算点的贡献,每个点会被计算 \(deep_x\) 次,那么答案就化为 \(\sum\limits_xdeep_x\) , 再进行一步转化, \(deep_x\) 等价于 \(\sum_\limits y[y是x的祖先]\) (当 \(x=y\) 时也成立) 。我们可以画图发现,点对 \((x,y)\) 会产生贡献当且仅当 \(y\) 被选中时 \(x\) 和 \(y\) 在一个连通块内,也就是 \(y\) 是在原树中 \(x\rightarrow y\) 路径(包括端点)上第一个被选中的点,举个例子

我们现在考虑 \((3,1)\) 的贡献,如果我们按照 \(1,2,3\) 或 \(1,3,2\) 的顺序,那么1就是3的祖先,会产生贡献,而如果是 \(2,1,3\) \(2,3,1\) \(3,1,2\) \(3,2,1\) 就都不会产生贡献(点对是有序的)。
显然,这个的概率是 \(\frac{1}{dis(x,y)}\) 所以答案就是 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^n\frac{1}{dis(i,j)}\) 。
接下来我们把树上的做法扩展到基环树上,我们仍旧考虑点对对答案的贡献,分类讨论一下:
- 当 \(x,y\) 在同一棵树内,概率仍为 \(\frac{1}{dis(x,y)}\)
- 当路径 \(x\rightarrow y\) 经过环上的点时,有两种情况可以造成贡献,分别是直接删掉 \(y\) 或者先删掉环上的某一个点再删掉 \(y\) ,如图
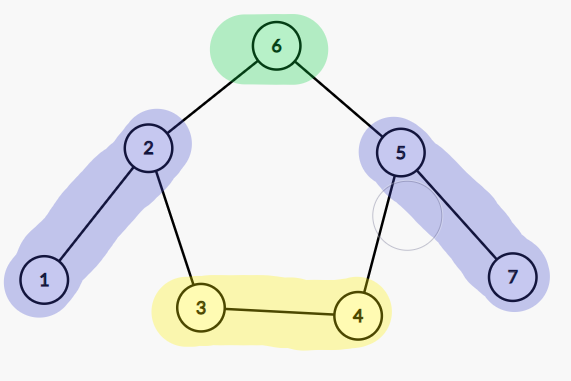
我们考虑点对 \((1,7)\) 设两个点到对应的树根的距离之和为 \(a\) (蓝色区域),两个点对应的树根将环切为两条链,链长为 \(b,c\) (绿色区域和黄色区域)。那么直接删掉 \(y\) 的概率为 \(\frac{1}{a+b+c}\) ,先切掉绿色区域后,剩余的绿色区域就已经不在 \(x\rightarrow y\) 这条路径上了,不会对后面造成影响 ,所以我们不需要管剩余的绿色区域,只需要看 \(y\) 是否是蓝色+黄色区域中第一个被切掉的点,这样总概率为 \(\frac{b}{a+b+c} \cdot \frac{1}{a+c}\) 。类似,先切掉黄色,再切掉 \(y\) 的概率为 \(\frac{c}{a+b+c}\cdot \frac{1}{a+b}\) 。
所以总概率为 \(\frac{1}{a+b+c}(1+\frac{b}{a+c}+\frac{c}{a+b})\) 。实现上我们只需要找到环然后暴力枚举计算答案就可以了。还需要写一个lca,代码中用倍增实现,所以复杂度为 \(O(n^2\log n)\)
code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #include<bits/stdc++.h>
using namespace std;
int target[6005],pre[6005],last[3005],tot,fa[3005],belong[3005],
deep[3005],f[3005][12],index[3005];
bool cir[3005];
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
void add(int x,int y)
{
target[++tot]=y;
pre[tot]=last[x];
last[x]=tot;
}
void dfs(int x,int fa)
{
if(cir[x]){index[x]=1;return;}
for(int i=last[x];i;i=pre[i])
{
int tar=target[i];
if(tar==fa)continue;
dfs(tar,x);
if(cir[tar])cir[x]=1,index[x]=index[tar]+1;
}
}
void dfs2(int x,int fa,int z)
{
deep[x]=deep[fa]+1;belong[x]=z;
f[x][0]=fa;
for(int i=last[x];i;i=pre[i])
{
int tar=target[i];
if(tar==fa||cir[tar])continue;
dfs2(tar,x,z);
}
}
int lca(int x,int y)
{
if(deep[x]<deep[y])swap(x,y);
for(int k=11;k>=0;k--)if(deep[f[x][k]]>=deep[y])x=f[x][k];
if(x==y)return x;
for(int k=11;k>=0;k--)if(f[x][k]!=f[y][k])x=f[x][k],y=f[y][k];
return f[x][0];
}
int main()
{
int n,x,y,len;
scanf("%d",&n);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=n;i++)
{
scanf("%d%d",&x,&y);
x++,y++;
int fx=find(x),fy=find(y);
if(fx!=fy)fa[fx]=fy;
else cir[y]=1,dfs(x,0),len=index[x];
add(x,y),add(y,x);
}
for(int i=1;i<=n;i++)if(cir[i])dfs2(i,0,i);
for(int k=1;k<=11;k++)
for(int i=1;i<=n;i++)
f[i][k]=f[f[i][k-1]][k-1];
double ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(belong[i]==belong[j])
{
int l=lca(i,j);
ans+=1.0/(deep[i]+deep[j]-2*deep[l]+1);
}
else
{
int a=deep[i]+deep[j],b=abs(index[belong[i]]-index[belong[j]])-1,c=len-b-2;
ans+=1.0/(a+b+c)*(1+1.0*b/(a+c)+1.0*c/(a+b));
}
}
printf("%.8lf",ans);
return 0;
}
|

